![]()
Pada tulisan ini saya akan membahas mengenai aplikasi integral yaitu untuk menentukan volume benda putar. Benda putar adalah suatu daerah yang dibatasi oleh kurva dan kemudian diputar sejauh 360 derajat.
Dalam volume benda putar ada dua bagian yaitu :
Mengelilingi Sumbu x
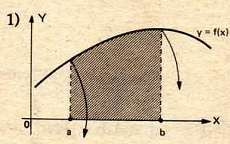
perhatikan gambar ilustrasi di atas. Luasan di bawah kurva y=f(x) jika diputar dengan sumbu putar dengan titik batas a dan b akan menghasilkan sebuah silinder dengan tinggi selisih b dan a
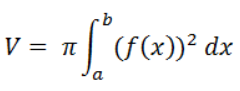
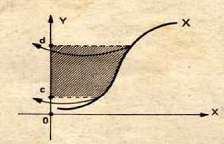
Mengelilingi Sumbu y
Untuk volume benda putar dengan sumbu putar adalah sumbu y, soba harus mengubah persamaan grafik yang semula y yang merupakan fungsi dari x menjadi kebalikannya x menjadi fungsi dari y.
y = f(x) menjadi x = f(y).
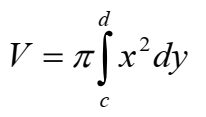
Selanjutnya juga dibatasi oleh 1 kurva atau 2 kurva
Jika ada sebuah luasan yang dibatasi oleh dua kurva yaitu f(x) dan g(x) dimana |f(x)| ≥ |g(x)| dengan interval [a,b] diputar mengelilingi sumbu x, maka volume benda putar tersebut dapat dihitung dengan rumus:
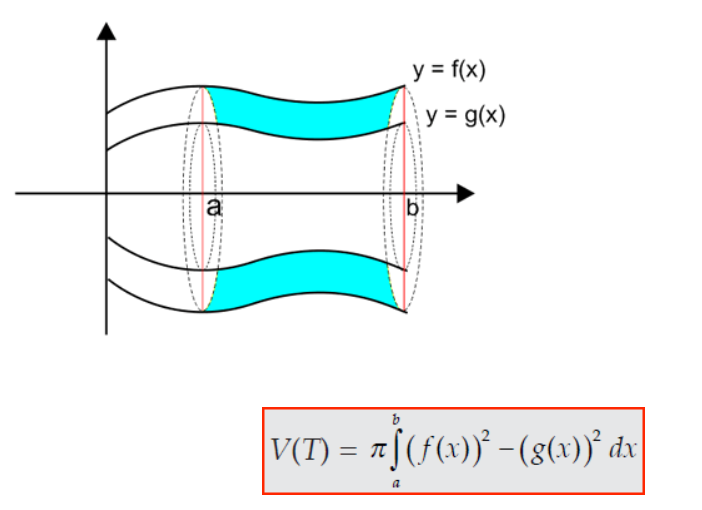
Sama prinsipnya dengan yang di atas , jika ada sebuah luasanyang terbentuk dari dua buah kurva x = f(y) dan x = g(y) dan interval [a.b] yang diputar mengitari sumbu y maka volume yang dihasilkan dapat dicari dengan rumus
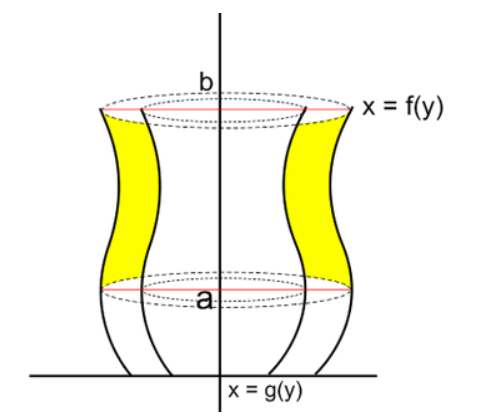
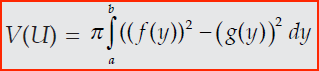
untuk penjelasan lebih lengkap simak video berikut ini :
